「計時」不能評估演算法效能?

Posted on In

在學習或撰寫演算法程式時，會遇到一個問題是:「我怎麼知道這段程式碼快不快?」。直覺上的做法，或許就是直接把「程式跑起來，然後計時」，但這個方法其實隱藏了陷阱，因為「秒數」本身並不一定能公平反映程式效率。

兩大問題

「計時」這種方法其實有兩個大問題。

硬體差異

同一段程式，如果換不同電腦，跑出來的時間會有差。

  • Linux (Colab): 95 秒
  • Windows 11 (桌機): 138 秒

同樣的演算法，因為 CPU 核心數、作業系統、甚至快取機制不同，差了 40 秒。所以，單純看「秒數」並不公平。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
import psutil, platform, sys, time, os

def sys_info():
    info = {
        "python": sys.version.split()[0],
        "platform": platform.platform(),
        "processor": platform.processor() or platform.machine(),
        "cpu_count": os.cpu_count()
    }
    if psutil:
        try:
            freq = psutil.cpu_freq()
            if freq:
                info["cpu_freq_MHz"] = round(freq.max or freq.current, 1)
        except Exception:
            pass
    return info

def process_data(n: int) -> int:
    total = 0
    for i in range(n):
        total += i * i
    return total

def measure(n):
    start = time.perf_counter()
    result = process_data(n)
    end = time.perf_counter()
    print(f"n={n}, result={result}, time={end - start:.6f} 秒")
1
2
3
4
5
6
7
8
print("== System Info ==")
print(sys_info(), "\n")
# {'python': '3.12.11', 'platform': 'Linux-6.1.123+-x86_64-with-glibc2.35', 'processor': 'x86_64', 'cpu_count': 2, 'cpu_freq_MHz': 2200.2}
# {'python': '3.13.3', 'platform': 'Windows-11-10.0.22631-SP0', 'processor': 'Intel64 Family 6 Model 140 Stepping 1, GenuineIntel', 'cpu_count': 8, 'cpu_freq_MHz': 2419.0}

measure(int(1e9))
# n=1000000000, result=333333332833333333500000000, time=94.522565 秒
# n=1000000000, result=333333332833333333500000000, time=138.439304 秒

資料規模

同一段程式，如果輸入資料量不同，結果也會有差。

  • 1,000 萬筆約 0.87 秒
  • 放大到 10 億筆就要約 100 秒

輸入放大 100 倍，執行時間也差不多放大 100 倍。這並不是電腦突然「變慢」，而是因為這段程式是線性時間 O(n)，處理每一筆資料都要一步，n 倍資料就要 n 倍時間。所以，「資料量」也會影響到效能。

1
2
3
4
5
6
7
8
9
10
11
12
13
import time

def process_data(n):
    total = 0
    for i in range(n):
        total += i * i
    return total

def measure(n):
    start = time.perf_counter()
    result = process_data(n)
    end = time.perf_counter()
    print(f"n={n}, result={result}, time={end - start:.6f} 秒")
1
2
3
4
5
measure(10_000_000) #千萬
measure(int(1e9)) #10億

# n=10000000, result=333333283333335000000, time=0.866556 秒
# n=1000000000, result=333333332833333333500000000, time=100.171150 秒

因此，計時並不能真正反映演算法的效率，因為結果混合了硬體、作業系統、程式語言、以及資料規模等外部因素。更科學的做法，則是用「時間複雜度(Time Complexity)」與「空間複雜度(Space Complexity)」這兩個標準，來評估演算法的好壞。

理想目標就是: 花最少的時間，用最少的空間。但有時這兩個目標會互相衝突，就要思考怎麼「取捨(Trade-off)」。

i-want-all

基礎定義

大O符號

在演算法分析中， 「大O符號 (Big O notation)」 是描述「演算法複雜度」的標準語言。它用來表達: 當輸入資料量增加時，演算法的操作次數或記憶體需求會如何隨之成長。

這張圖清楚地展示了不同複雜度在輸入規模 n 增加時，所帶來的運算量差異。

  • 顏色越偏紅，代表效能越差。
  • 顏色越偏綠，代表效能越好。

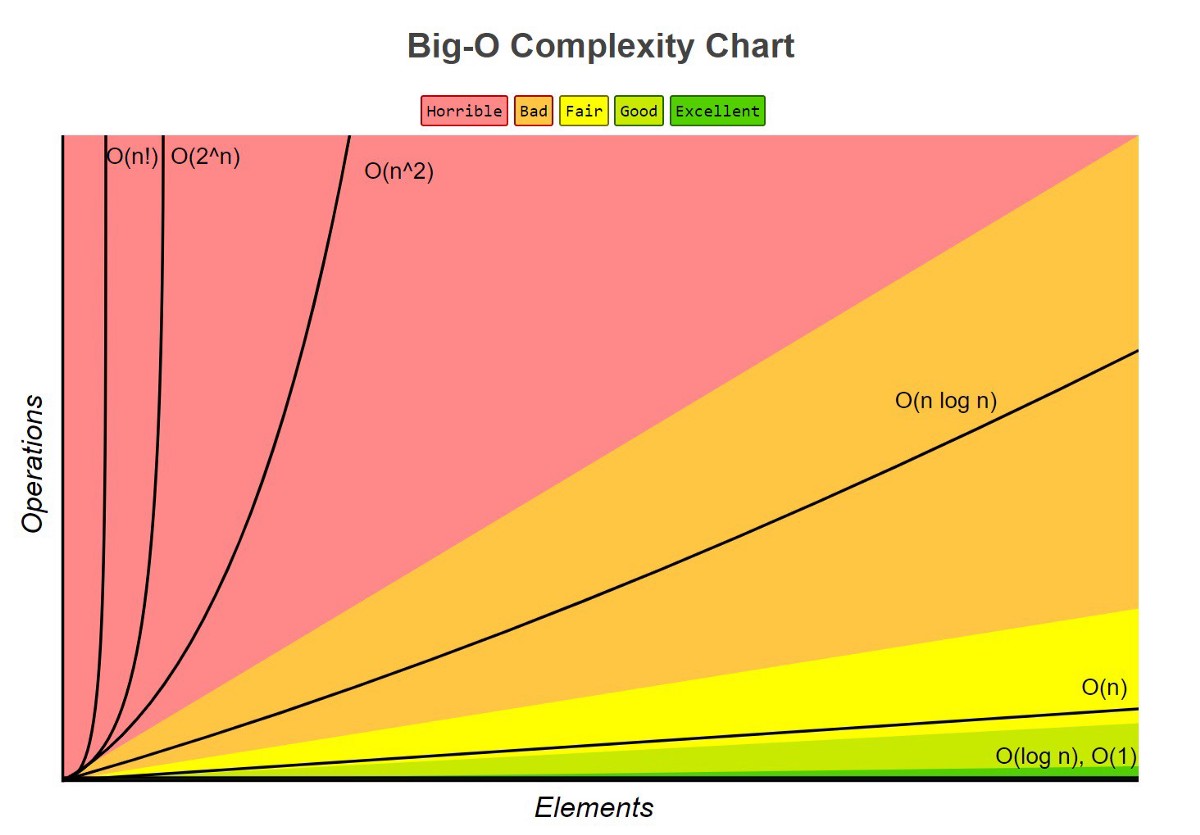
big-o-complexity-chart

1
2
3
4
5
6
7
8
9
# 由好到差排列複雜度
O(1) #常數
O(log n) #對數
O(n) #線性
O(n log n) #線性對數
O(n^2) #平方
O(n^k) #多項式
O(2^n) #指數
O(n!) #階乘

時間複雜度

隨輸入規模 n 增長時，基本操作次數的成長趨勢。

同樣的程式在不同電腦上執行時間差異很大，如 Colab: 95秒 vs Windows 11: 138秒，因此不是用「程式跑幾秒」，而是以「程式執行了多少次基本操作」來客觀衡量演算法效率。

核心概念是當輸入資料量 n 增加時，演算法需要多少次基本操作來完成，關注的是隨著 n 成長的趨勢，而不是實際執行的秒數。舉例來說:

  • 基本操作次數固定，不隨 n 變化，時間複雜度是常數時間 O(1)。
  • 遍歷 n 個元素需要 n 次，時間複雜度是線性時間 O(n)。
  • 雙層迴圈處理 n 個元素的所有配對，約需要 n² 次，時間複雜度是平方時間 O(n²)。

空間複雜度

隨輸入規模 n 增長時，額外記憶體的成長趨勢。

空間複雜度指執行一個演算法所需的記憶體空間，通常不包含輸入資料本身的空間，只計算演算法額外使用的記憶體。

核心概念是當輸入資料量 n 增加時，演算法需要分配多少額外的儲存空間。舉例來說:

  • 僅使用固定數量的變數，額外空間不隨 n 增長，空間複雜度是常數空間 O(1)。
  • 建立一個長度為 n 的結構，空間隨著 n 成長，空間複雜度是線性空間 O(n)。
  • 建立一個 n × n 的二維結構，空間隨著 n² 成長，空間複雜度是平方空間 O(n²)。

複雜度分析更科學?

複雜度分析的優勢在於:

  1. 無關硬體: 不受 CPU、記憶體、作業系統影響。
  2. 無關語言: Python、Java、C++ 都適用同樣的分析。
  3. 可規模比較: 可以客觀比較不同演算法在大資料下的表現。
  4. 預測能力: 能預測演算法在更大資料集上的行為。

所以當一個演算法是 O(n²)，就意味著無論在什麼硬體上運行，當輸入規模增大時，執行時間都會以平方級別成長。這是一個客觀、可預測、可比較的標準。

進階概念預告🔜

在理解了為什麼需要複雜度分析之後，下一篇我們將一起解鎖:

  • 透過 LeetCode 題目，逐步分析時間複雜度
  • 看看不同複雜度在演算法實戰中的應用情境

準備好來點 LeetCode 了嗎?

👇 點此免費訂閱，不錯過任何更新